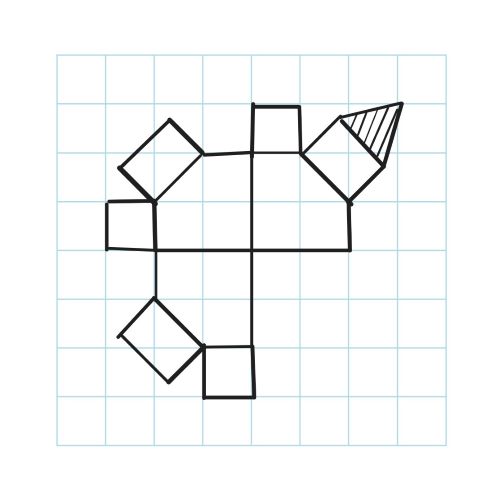
問題文
ある立体の展開図を、幅が $3\mathrm{cm}$ の方眼紙にかくと、下の図の太線のようになりました。斜線をつけた三角形は正三角形です。また、正方形でない四角形の面はすべて長方形です。
この立体の体積は $\mathrm{cm^3}$ です。
(2021 灘中 1日目12番)
$$153$$
※ この答えは学校側が公表したものではありません。個人が作成した非公式の答えです。
コード
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as ani
from scipy.spatial.transform import Rotation
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
#紙の準備
fig = plt.figure()
ax=fig.add_subplot(projection='3d')
ax.set_title("2021灘中算数 1日目12番")
ax.set_box_aspect((1,1,1))
ax.axis("off")
#展開図の準備
soleX = [ 0, 0,-1,-2,-2]
soleY = [ 0, 2, 2, 1, 0]
soleZ = [ 0, 0, 0, 0, 0]
sole = list(zip(soleX,soleY,soleZ))
backLX = [ 0, 2, 2, 1, 0]
backLY = [ 0, 0, 1, 2, 2]
backLZ = [ 0, 0, 0, 0, 0]
backL = list(zip(backLX,backLY,backLZ))
backRX = [ 0, 0,-1,-2,-2]
backRY = [ 0,-2,-2,-1, 0]
backRZ = [ 0, 0, 0, 0, 0]
backR = list(zip(backRX,backRY,backRZ))
frontLX = [ 2,2+1/np.sqrt(2),1+1/np.sqrt(2),1]
frontLY = [ 1,1+1/np.sqrt(2),2+1/np.sqrt(2),2]
frontLZ = [ 0, 0, 0, 0]
frontL = list(zip(frontLX,frontLY,frontLZ))
frontCX = [-2,-1,-1-1/np.sqrt(2),-2-1/np.sqrt(2)]
frontCY = [ 1, 2, 2+1/np.sqrt(2), 1+1/np.sqrt(2)]
frontCZ = [ 0, 0, 0, 0]
frontC = list(zip(frontCX,frontCY,frontCZ))
frontRX = [-2,-2-1/np.sqrt(2),-1-1/np.sqrt(2),-1]
frontRY = [-1,-1-1/np.sqrt(2),-2-1/np.sqrt(2),-2]
frontRZ = [ 0, 0, 0, 0]
frontR = list(zip(frontRX,frontRY,frontRZ))
sideLX = [ 0, 1, 1, 0]
sideLY = [ 2, 2, 3, 3]
sideLZ = [ 0, 0, 0, 0]
sideL = list(zip(sideLX,sideLY,sideLZ))
sideRX = [-2,-2,-3,-3]
sideRY = [ 0, 1, 1, 0]
sideRZ = [ 0, 0, 0, 0]
sideR = list(zip(sideRX,sideRY,sideRZ))
roofX = [ 0,-1,-1, 0]
roofY = [-2,-2,-3,-3]
roofZ = [ 0, 0, 0, 0]
roof = list(zip(roofX,roofY,roofZ))
triX = [2+1/np.sqrt(2),1+1/np.sqrt(2),3/2+1/np.sqrt(2)+np.sqrt(3)/2]
triY = [1+1/np.sqrt(2),2+1/np.sqrt(2),3/2+1/np.sqrt(2)+np.sqrt(3)/2]
triZ = [ 0, 0, 0]
tri = list(zip(triX,triY,triZ))
#立体の描画
polys0 = [sole,backL,backR,frontL,frontC,frontR,sideL,sideR,roof,tri]
fcs = ["darkorange","darkorange","darkorange","gold","gold","gold","darkorange","darkorange","darkorange","darkkhaki"]
col = Poly3DCollection(polys0,facecolors=fcs,edgecolor="saddlebrown")
ax.add_collection3d(col)
#面を回転させる関数
def rot(poly,rotvec,transvec):
length = len(poly)
rot = Rotation.from_rotvec(rotvec)
XYZ = np.array(poly).T
trans = np.tile(transvec,(length,1)).T
rotXYZ = rot.as_matrix() @ (XYZ+trans)
rotpoly = (rotXYZ-trans).T
return rotpoly
#紙を折っていく関数
def ROT(polys,rotvecs,transvecs):
rotpolys = [polys[0]]
for i in range(len(polys)-1):
rotpoly = rot(polys[i+1],rotvecs[i],transvecs[i])
rotpolys += [rotpoly]
return rotpolys
#折り1回目
def fold1(i,polys):
theta = np.linspace(0,np.pi/2,100)[i]
n1 = np.array([0,-theta,0])
v1 = np.array([0,0,0])
n2 = np.array([-theta,0,0])
v2 = np.array([0,0,0])
n3 = np.array([theta/np.sqrt(2),theta/np.sqrt(2),0])
v3 = np.array([3/2,-3/2,0])
n4 = np.array([0,theta,0])
v4 = np.array([2,0,0])
ns = [n1,n2,n1,n3,n2,n1,n4,n2,n1]
vs = [v1,v2,v1,v3,v2,v1,v4,v2,v1]
rotpolys = ROT(polys,ns,vs)
col.set_verts(rotpolys)
return rotpolys
polys1=fold1(99,polys0)
#折り2回目
def fold2(i,polys):
theta = np.linspace(0,np.pi/2,100)[i]
n0 = np.array([0,0,0])
v0 = np.array([0,0,0])
n1 = np.array([0,-theta/np.sqrt(2),theta/np.sqrt(2)])
v1 = np.array([0,-3/2,-3/2])
n2 = np.array([-theta/np.sqrt(2),0,-theta/np.sqrt(2)])
v2 = np.array([3/2,0,-3/2])
n3 = np.array([0,0,theta])
v3 = np.array([0,-2,0])
n4 = np.array([-theta,0,0])
v4 = np.array([0,0,-2])
ns = [n0,n0,n1,n0,n2,n3,n0,n4,n1]
vs = [v0,v0,v1,v0,v2,v3,v0,v4,v1]
rotpolys = ROT(polys,ns,vs)
col.set_verts(rotpolys)
return rotpolys
polys2=fold2(99,polys1)
#折り3回目
def fold3(i,polys):
theta = np.linspace(0,np.arcsin(1/np.sqrt(3)),50)[i]
n0 = np.array([0,0,0])
v0 = np.array([0,0,0])
n1 = np.array([0,-theta/np.sqrt(2),theta/np.sqrt(2)])
v1 = np.array([1,-3/2,-3/2])
ns = [n0,n0,n0,n0,n0,n0,n0,n0,n1]
vs = [v0,v0,v0,v0,v0,v0,v0,v0,v1]
rotpolys = ROT(polys,ns,vs)
col.set_verts(rotpolys)
return rotpolys
#最後のお願い
commentdic={
"ha" : "center",
"va" : "center",
"size" : 20,
"color" : "white",
"fontfamily": "Meiryo",
}
commentbgdic={
"facecolor" : "black",
"pad" : 300,
}
msg = "体積の出し方は\nお母さんかお父さんに\n聞いてみてね ♥\n\n( ゚∀ ゚)"
txt = fig.text(0.5,0.5,msg,
fontdict=commentdic,bbox=commentbgdic)
#台本
def update(k):
if k<50:
txt.set_visible(False)
ax.set_xlim(-3,3)
ax.set_ylim(-3,3)
ax.set_zlim(-2,4)
ax.view_init(90,-90)
fold1(0,polys0)
elif k<250:
t = (k-50)/199
ax.set_xlim(-3+t,3)
ax.set_ylim(-3+t,3)
ax.set_zlim(-2+t,4)
ax.view_init(90-60*t,-90+210*t)
fold1(0,polys0)
elif k<350:
fold1(k-250,polys0)
elif k<400:
t = (k-350)/49
ax.set_xlim(-2,3-2*t)
ax.set_ylim(-2+t,3-t)
ax.set_zlim(-1+t,4-t)
fold2(0,polys1)
elif k<500:
fold2(k-400,polys1)
elif k<550:
t = (k-500)/49
ax.set_xlim(-2,1-0.8*t)
ax.set_ylim(-1+0.8*t,2)
ax.set_zlim(0,3-0.8*t)
fold3(0,polys2)
elif k<600:
fold3(k-550,polys2)
elif k<750:
t = (k-600)/149
ax.view_init(30,120+375*t)
fold3(49,polys2)
elif k<850:
t = (k-750)/99
ax.view_init(30+240*t,135)
fold3(49,polys2)
elif k<900:
t = (k-850)/49
ax.view_init(-90+120*t,135)
fold3(49,polys2)
elif k<1000:
fold3(49,polys2)
else:
txt.set_visible(True)
#上演
mov = ani.FuncAnimation(fig,update,1100,interval=100)
plt.show()