問題文
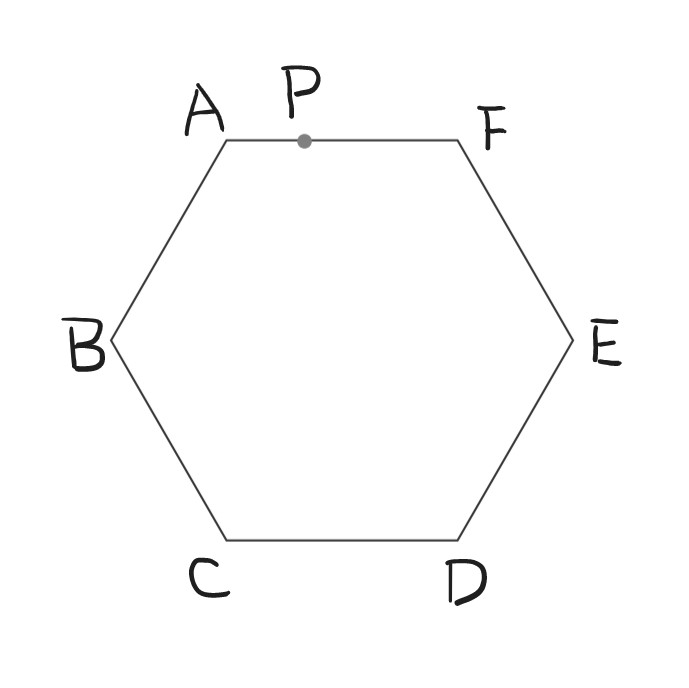
図のような、1辺の長さが $1\mathrm{cm}$ の正六角形 $\mathrm{ABCDEF}$ の周上に、次のような点 $\mathrm{P}$ と点 $\mathrm{Q}$ があります。
・点 $\mathrm{P}$ は辺 $\mathrm{AF}$ 上にあり、 $\mathrm{AP}:\mathrm{PF}=1:2$ です。
・点 $\mathrm{Q}$ は頂点 $\mathrm{A}$ を出発し、正六角形の周上を反時計回りに分速 $1\mathrm{cm}$ で動きます。点 $\mathrm{Q}$ は、頂点 $\mathrm{B,C,D,E}$ をこの順で通り、頂点 $\mathrm{A}$ を出発した5分後に頂点 $\mathrm{F}$ で止まります。
点 $\mathrm{Q}$ が頂点 $\mathrm{A}$ や頂点 $\mathrm{F}$ にいるときを除いて、正六角形は直線 $\mathrm{PQ}$ によって2つの部分に分けられます。この2つの部分のうち、一方の面積が他方の面積の2倍になるのは、点 $\mathrm{Q}$ が頂点 $\mathrm{A}$ を出発してから何分何秒後ですか。2つ答えなさい。
(2023 開成中 2番)
※ この答えは学校側が公表したものではありません。個人が作成した非公式の答えです。
コード
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as ani
import matplotlib.patches as patches
#定数の準備
s60 = np.sqrt(3)/2
ew = 2.0
ec = "0.5"
c1 = "darkorange"
c2 = "mediumblue"
#フォント辞書たち
commentdic = {
"size" : 14,
"ha" : "center",
"va" : "center",
"linespacing" : 2,
"fontfamily" : "Meiryo",
}
ratiodic = {
"size" : 15,
"color" : ec,
"alpha" : 0.0,
"ha" : "center",
"va" : "center",
"fontfamily" : "Meiryo",
}
lengthdic = {
"size" : 13,
"alpha" : 0.0,
"ha" : "center",
"va" : "center",
}
#紙の準備
left = -1.6
right = 1.6
bottom = -1.2
top = 1.2
fig = plt.figure()
fig.suptitle("2023開成中算数 2番",
color="0.5",ha="right",x=0.96,y=0.96)
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
for ax in [ax1,ax2]:
ax.set_xlim(left,right)
ax.set_ylim(bottom,top)
ax.set_aspect("equal")
ax.axis("off")
#正六角形の描画
verts = [np.array([np.cos(k*np.pi/3),np.sin(k*np.pi/3)]) for k in range(2,9)]
hexagon = patches.Polygon(verts[:6],fill=False,ec="0.8")
partL = patches.Polygon([(0,0)],fc=c1,alpha=0.2)
partR = patches.Polygon([(0,0)],fc=c2,alpha=0.2)
for obj in [hexagon,partL,partR]:
ax1.add_patch(obj)
#点の準備
p = np.array([-1/6,np.sqrt(3)/2])
q1 = 5/6*verts[2]+1/6*verts[3]
q2 = 4/5*verts[3]+1/5*verts[4]
lu = np.array([-3/2, s60])
ld = np.array([-3/2,-s60])
ru = np.array([ 3/2, s60])
rd = np.array([ 3/2,-s60])
Q, = ax1.plot([],color="royalblue",marker="o",zorder=20)
points = []
for ax in [ax1,ax2]:
points += ax.plot(p[0],p[1],q1[0],q1[1],q2[0],q2[1],
color=ec,marker="o",zorder=10,alpha=0.0)
points[0].set_alpha(1.0)
#補足説明の言葉たち
text1u = ax1.text((left+right)/2,top+0.3,"",fontdict=commentdic)
text1d = ax1.text((left+right)/2,bottom-0.3,"",fontdict=commentdic)
text2d = ax2.text(0.20,bottom-0.6,"$:\\qquad\\quad\\;=\\quad:$",fontdict=lengthdic)
comment = ax2.text((left+right)/2,(bottom+top)/2,
"正六角形が $1:2$\nに分割される瞬間\nをもとめましょう",
fontdict=commentdic)
#杏仁豆腐
rulers = [points[3]]
for i in range(-2,3):
rulers += ax2.plot([left,right],[s60*i,s60*i],
[left,right],[ np.sqrt(3)*(left-i), np.sqrt(3)*(right-i)],
[left,right],[-np.sqrt(3)*(left-i),-np.sqrt(3)*(right-i)],
color="0.8",lw=0.8,zorder=-10,alpha=0.0)
#面積比を準備する関数
def set_area(verts,ratio):
outline = patches.Polygon(verts,fc="0.95",lw=ew,ec=ec,alpha=0.0)
ax2.add_patch(outline)
g = np.average(verts,axis=0)
str_ratio = chr(10101+ratio)
txt_ratio = ax2.text(g[0],g[1],str_ratio,fontdict=ratiodic)
area = [outline,txt_ratio]
return area
#面積比たち
areas1 = []
for i in range(6):
area = set_area([(0,0),verts[i],verts[i+1]],1)
areas1 += area
areas2 = set_area(verts[0:6],6)
areas2 += set_area(np.vstack([lu,verts[0:2]]),1)
areas2 += set_area(np.vstack([rd,verts[3:5]]),1)
areas3 = set_area(np.vstack([p,verts[0:3],q1]),2)
areas3 += set_area(np.vstack([q1,verts[3:6],p]),4)
areas3 += set_area(np.vstack([lu,verts[0:2]]),1)
areas3 += set_area(np.vstack([rd,verts[3:5]]),1)
areas4 = set_area(np.vstack([p,lu,verts[2],q1]),3)
areas4 += set_area(np.vstack([q1,rd,verts[5],p]),5)
areas4 += [points[1],points[4]]
areas5 = set_area(np.vstack([p,verts[0:4],q2]),4)
areas5 += set_area(np.vstack([q2,verts[4:6],p]),2)
areas5 += set_area(np.vstack([ld,verts[1:3]]),1)
areas5 += set_area(np.vstack([ru,verts[4:6]]),1)
areas6 = set_area(np.vstack([p,q2,ru]),3)
areas6 += set_area(np.vstack([ld,verts[1:3]]),1)
areas6 += [points[2],points[5]]
seq_areas = [areas1,areas2,areas3,areas4,areas5,areas6]
#長さたち
group1a = ax2.plot([-3/2,-1/6],[ s60, s60],c1,
[-1/2,-1/3],[-s60,-s60],c1,
[-1/6, 1/2],[ s60, s60],c2,
[-1/3, 3/2],[-s60,-s60],c2,
lw=ew,alpha=0.0)
group1a += [
ax2.text( -5/6, s60+0.3,"$\\frac{4}{3}$",color=c1,fontdict=lengthdic),
ax2.text( 1/6, s60+0.3,"$\\frac{2}{3}$",color=c2,fontdict=lengthdic),
]
group1b = [
ax2.text(-5/12,-s60-0.3,"$\\frac{1}{6}$",color=c1,fontdict=lengthdic),
ax2.text( 7/12,-s60-0.3,"$\\frac{11}{6}$",color=c2,fontdict=lengthdic),
ax2.text(-1.00,bottom-0.6,"$\\frac{4}{3}+\\frac{1}{6}$",color=c1,fontdict=lengthdic),
ax2.text(-0.05,bottom-0.6,"$\\frac{2}{3}+\\frac{11}{6}$",color=c2,fontdict=lengthdic),
ax2.text( 0.80,bottom-0.6,"$3$",color=c1,fontdict=lengthdic),
ax2.text( 1.25,bottom-0.6,"$5$",color=c2,fontdict=lengthdic),
text2d,
]
group2a = ax2.plot([-3/2,-1/2],[-s60,-s60],c1,
[-3/2, -1],[-s60, 0],c1,
[ 3/2,-1/6],[ s60, s60],c2,
[3/2,3/5],[s60,-4/5*s60],c2,
lw=ew,alpha=0.0)
group2a += [
ax2.text(-1,-s60-0.3,"$1$",color=c1,fontdict=lengthdic),
ax2.text(-5/4-0.2,-s60/2+0.2,"$1$",color=c1,fontdict=lengthdic),
]
group2b = [
ax2.text(2/3,s60+0.3,"$\\frac{5}{3}$",color=c2,fontdict=lengthdic),
ax2.text(21/20+0.2,s60/10-0.2,"$\\frac{9}{5}$",color=c2,fontdict=lengthdic),
ax2.text(-1.00,bottom-0.6,"$1\\times1$",color=c1,fontdict=lengthdic),
ax2.text(-0.05,bottom-0.6,"$\\frac{5}{3}\\times\\frac{9}{5}$",color=c2,fontdict=lengthdic),
ax2.text( 0.80,bottom-0.6,"$1$",color=c1,fontdict=lengthdic),
ax2.text( 1.25,bottom-0.6,"$3$",color=c2,fontdict=lengthdic),
text2d,
]
#点Qを動かす関数
def moving_Q(i):
hen = i//600
k = (i-600*hen)/599
q = (1-k)*verts[hen]+k*verts[hen+1]
Q.set_data(q[0],q[1])
partL.set_xy(np.vstack([p,verts[0:hen+1],q]))
partR.set_xy(np.vstack([q,verts[hen+1:6],p]))
#お気に入りのイージング関数
def easing(x):
if x<0.0:
return 0
elif x<0.5:
return 2**(20*x-10)/2
elif x<1.0:
return (2-2**(-20*x+10))/2
else:
return 1
#いろんなものを見せたり消したりする関数
def set_objs_alpha(k,objs,disappear=False):
if disappear == False:
alpha = easing(k/99)
else:
alpha = 1-easing(k/99)
for obj in objs:
obj.set_alpha(alpha)
#セクションを判定する関数
def section(i):
n = np.argmin(~(i<endings))
keys = list(periods.keys())
key = keys[n]
if n == 0:
k = i
else:
k = i-endings[n-1]
return key,k
#台本の構成
periods = {"N0":100,"O1":100,
"S1":100,"N1":100,"T2":100,"N2":100,
"T3":100,"N3":100,"T4":100,"N4":100,
"I1":100,"I2":100,"I3":100,
"T5":100,"N5": 50,"T6":100,"N6": 50,
"I4":100,"I5":100,"I6": 20,"I7":100,
"D7":100,"E1": 98,}
endings = np.cumsum(list(periods.values()))
#上演
def update(i):
key,k = section(i)
n = int(key[-1])-1
if "E1" == key:
moving_Q(2019+10*k)
t = 203+k
else:
moving_Q(i)
t = i//10
second = str(t%60).rjust(2,"0")
minute = str(t//60)
text1u.set_text(minute+" 分 "+second+" 秒")
if "T" in key:
set_objs_alpha(k,seq_areas[n-1],disappear=True)
set_objs_alpha(k,seq_areas[n])
if "O1" == key:
set_objs_alpha(k,[comment],disappear=True)
set_objs_alpha(k,rulers)
if "S1" == key:
set_objs_alpha(k,seq_areas[n])
elif "I1" == key:
set_objs_alpha(k,group1a)
elif "I2" == key:
set_objs_alpha(k,group1b)
elif "I3" == key:
text1d.set_text("残り "+str(130-t)+" 秒")
elif "T5" == key:
set_objs_alpha(k,group1a,disappear=True)
set_objs_alpha(k,group1b,disappear=True)
elif "I4" == key:
set_objs_alpha(k,group2a)
elif "I5" == key:
set_objs_alpha(k,group2b)
elif "I7" == key:
text1d.set_text("残り "+str(192-t)+" 秒")
elif "D7" == key:
set_objs_alpha(k,seq_areas[n-1],disappear=True)
set_objs_alpha(k,group2a,disappear=True)
set_objs_alpha(k,group2b,disappear=True)
set_objs_alpha(k,rulers,disappear=True)
set_objs_alpha(k,[comment])
if i==1300:
text1d.set_text("")
fig.set_facecolor("gold")
elif i==1310:
fig.set_facecolor("w")
elif i==1920:
text1d.set_text("")
fig.set_facecolor("gold")
elif i==1930:
fig.set_facecolor("w")
comment.set_text("もう過ぎ去ったので\nあとは早送りします")
mov = ani.FuncAnimation(fig,update,endings[-1],interval=100)
plt.show()