問題文
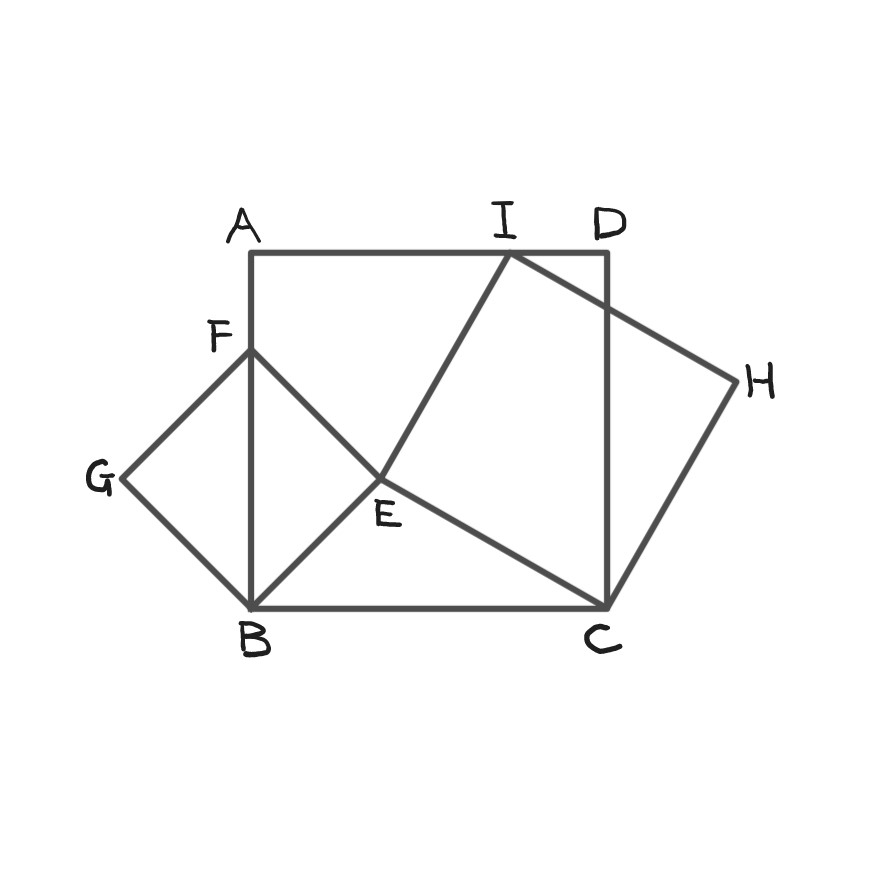
図の四角形 $\mathrm{ABCD,BEFG,CHIE}$ はすべて正方形です。また、 $\mathrm{F}$ は辺 $\mathrm{AB}$ 上に、 $\mathrm{I}$ は辺 $\mathrm{AD}$ 上にあります。正方形 $\mathrm{CHIE}$ の面積が $65\,\mathrm{cm^2}$ 、四角形 $\mathrm{AFEI}$ の面積と三角形 $\mathrm{BCE}$ の面積の和が $56\,\mathrm{cm^2}$ のとき、正方形 $\mathrm{BEFG}$ の面積は $\mathrm{cm^2}$ です。(2023 灘中 1日目10番)
$$32$$
※ この答えは学校側が公表したものではありません。個人が作成した非公式の答えです。
コード
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as ani
from matplotlib.patches import Polygon
#紙の準備
left = -6
right = 40
bottom = -9
top = 17
fig = plt.figure()
fig.suptitle("2023灘中 1日目10番",
color="0.6",ha="right",x=0.96,y=0.08)
ax = fig.add_subplot(111)
ax.set_xlim(left,right)
ax.set_ylim(bottom,top)
ax.set_aspect("equal")
ax.axis("off")
#色のセッティング
col0 = "yellowgreen"
col1 = "deepskyblue"
col2 = "orangered"
#正方形たちの準備
S0,= ax.plot([0,11,11,0,0],[0,0,11,11,0],
color="tan",linewidth=3)
v0 = [[0,0],[4,4],[0,8],[-4,4]]
v1 = [(4,4),(11,0),(15,7),(8,11)]
v2 = [(4,11),(4,4),(8,11)]
v3 = [(4,0),(11,0),(4,4)]
v4 = [(4,11),(4,4),(0,8),(0,11)]
v5 = [(4,0),(4,4),(0,0)]
P0 = Polygon(v0,fc=col0)
P1 = Polygon(v1,fc=col1)
P2 = Polygon(v2,fc=col2)
P3 = Polygon(v3,fc=col2)
P4 = Polygon(v4,fc=col2)
P5 = Polygon(v5,fc=col2)
for patch in [P0,P1,P2,P3,P4,P5]:
ax.add_patch(patch)
#解説パートの準備
fdic = {"va":"center","fontsize":12,"fontfamily":"HGSoeiKakupoptai","alpha":0}
txt0a = ax.text(18, 0,"緑",fontdict=fdic,fontsize=16,color="w")
txt0b = ax.text(21, 0,"の面積",fontdict=fdic)
txt0c = ax.text(26, 0,"$=$",fontdict=fdic)
txt0d = ax.text(28,-0.2,"?",fontdict=fdic)
obj0e = Polygon([(29,1.5),(29,-2.5),(33,1.5)],fc=col0,alpha=0)
ax.add_patch(obj0e)
txt0f = ax.text(33, 0,"$\\times\\:4$",fontdict=fdic)
txt0g = ax.text(26,-5,"$=32$",fontdict=fdic)
txt1a = ax.text(18,10,"青",fontdict=fdic,fontsize=16,color="w")
txt1b = ax.text(21,10,"の面積",fontdict=fdic)
txt1c = ax.text(26,10,"$=65$",fontdict=fdic)
txt1d = ax.text(30,10,"$=a\\times a+b\\times b$",fontdict=fdic)
txt1e = ax.text(30,10,"$=4\\times 4+7\\times 7$",fontdict=fdic)
txt2a = ax.text(18, 5,"赤",fontdict=fdic,fontsize=16,color="w")
txt2b = ax.text(21, 5,"の面積",fontdict=fdic)
txt2c = ax.text(26, 5,"$=56$",fontdict=fdic)
txt2d = ax.text(30, 5,"$=2\\times a\\times b$",fontdict=fdic)
txt2e = ax.text(30, 5,"$=2\\times 4\\times 7$",fontdict=fdic)
#面積を表記します
fdic = {"color":"white","ha":"center","va":"center","alpha":0}
waa = ax.text( 6.0, 2.0,"$16$",fontdict=fdic)
wab = ax.text( 6.0, 7.5,"$28$",fontdict=fdic)
wba = ax.text(11.5, 2.0,"$28$",fontdict=fdic)
wbb = ax.text(11.5, 7.5,"$49$",fontdict=fdic)
we = ax.text(30.3, 0.2,"$8$",fontdict=fdic)
#長さを表記する関数
def annotate_length(edge1,edge2,latex,answer,hv,position):
x = np.linspace(edge1,edge2,100)
y = 3*(x-edge1)*(x-edge2)/(edge2-edge1)**2+position
if hv == "hd":
px = x
py = y
tx = (edge1+edge2)/2
ty = position-3/4
elif hv == "hu":
px = x
py = -y+2*position
tx = (edge1+edge2)/2
ty = position+3/4
elif hv == "v":
px = y
py = x
tx = position-3/4
ty = (edge1+edge2)/2
p, = ax.plot(px,py,color="0.6",linewidth=1,alpha=0)
txt = ax.text(tx,ty,latex,
color="0.3",ha="center",va="center",
bbox=dict(facecolor="white",pad=0,linewidth=0),
visible=False,alpha=0)
ans = ax.text(tx,ty,"$"+str(answer)+"$",
color="0.3",ha="center",va="center",
alpha=0)
return p,txt,ans
#長さを表記します
ph1,th1,ah1 = annotate_length( 4, 8,"$a$",4,"hd",0)
ph2,th2,ah2 = annotate_length( 8,15,"$b$",7,"hd",0)
pv1,tv1,av1 = annotate_length( 0, 4,"$a$",4,"v",4)
pv2,tv2,av2 = annotate_length( 4,11,"$b$",7,"v",4)
phe,the,ahe = annotate_length(29,33,"$4$",4,"hu",1.5)
pve,tve,ave = annotate_length(-2.5,1.5,"$4$",4,"v",29)
#ポリゴンを組み換える関数
def change_verts(P,verts,new_xy):
verts.clear()
verts.extend(new_xy)
P.set_xy(verts)
#ポリゴンを動かす関数
def translate(k,P,verts,x,y,theta=0,vindex=0):
old_xy = np.array(verts,dtype=float)
new_xy = np.empty_like(old_xy)
anchor = np.array(verts[vindex],dtype=float)
R = np.array([[np.cos(k*theta),-np.sin(k*theta)],
[np.sin(k*theta), np.cos(k*theta)]])
for i in range(len(old_xy)):
new_xy[i] = R @ (old_xy[i]-anchor) + anchor + np.array([k*x,k*y])
P.set_xy(new_xy)
if k==1:
verts.clear()
verts.extend(new_xy)
#お気に入りのイージング関数
def easing(x):
if x<0.5:
return 2*x**2
else:
return 1-(-2*x+2)**2/2
#セクションの設定
ends = np.array([
30,60,90,120,150,180,240,300,
380,381,420,500,550,600,601,650,700,701,
750,800,850,900,950,1000,1050,1100,1150,
1151,1200,1250,1300,1400,1500])
#セクションを判定する関数
def section(i):
n = np.argmin(~(i<ends))
T = np.diff(ends)
if n == 0:
k = easing(i/(ends[0]-1))
elif T[n-1]==1:
k = np.nan
else:
k = easing((i-ends[n-1])/(T[n-1]-1))
return n,k
#台本
def update(i):
n,k = section(i)
if n==0:
txt1a.set_alpha(k)
txt1a.set_bbox(dict(facecolor=col1,boxstyle="round",linewidth=0,alpha=k))
txt1b.set_alpha(k)
elif n==1:
txt1c.set_alpha(k)
elif n==2:
txt2a.set_alpha(k)
txt2a.set_bbox(dict(facecolor=col2,boxstyle="round",linewidth=0,alpha=k))
txt2b.set_alpha(k)
elif n==3:
txt2c.set_alpha(k)
elif n==4:
txt0a.set_alpha(k)
txt0a.set_bbox(dict(facecolor=col0,boxstyle="round",linewidth=0,alpha=k))
txt0b.set_alpha(k)
elif n==5:
txt0c.set_alpha(k)
txt0d.set_alpha(k)
elif n==6:
pass
elif n==7:
S0.set_alpha(1-k)
elif n==8:
translate(k,P5,v5,0,0,-np.pi/2,1)
elif n==9:
change_verts(P4,v4,[(0,11),(0,4),(4,11)])
change_verts(P5,v5,[(4,4),(4,11),(0,4)])
elif n==10:
translate(k,P4,v4,-1,0)
translate(k,P5,v5,-1,0)
elif n==11:
translate(k,P4,v4,0,1,-np.pi/2,2)
translate(k,P5,v5,0,-12)
elif n==12:
translate(k,P4,v4,12,0)
translate(k,P5,v5,12,0)
elif n==13:
translate(k,P4,v4,0,-5)
translate(k,P5,v5,0,8)
elif n==14:
change_verts(P1,v1,[(4,0),(15,0),(15,11),(4,11)])
elif n==15:
translate(k,P4,v4,0,0,-np.pi/2,1)
elif n==16:
translate(k,P3,v3,4,0)
translate(k,P5,v5,4,0,np.pi/2,2)
elif n==17:
for txt in [th1,th2,tv1,tv2]:
txt.set_visible(True)
elif n==18:
for obj in [ph1,th1,ph2,th2,pv1,tv1,pv2,tv2]:
obj.set_alpha(k)
elif n==19:
txt1d.set_alpha(k)
elif n==20:
txt2d.set_alpha(k)
elif n==21:
txt1d.set_alpha(1-k)
txt1e.set_alpha(k)
elif n==22:
txt2d.set_alpha(1-k)
txt2e.set_alpha(k)
elif n==23:
for txt in [th1,th2,tv1,tv2]:
txt.set_alpha(1-k)
for ans in [ah1,ah2,av1,av2]:
ans.set_alpha(k)
elif n==24:
for ans in [waa,wab,wba,wbb]:
ans.set_alpha(k)
elif n==25:
pass
elif n==26:
txt0d.set_alpha(1-k)
elif n==27:
for txt in [the,tve]:
txt.set_visible(True)
elif n==28:
for obj in [obj0e,phe,ahe,pve,ave]:
obj.set_alpha(k)
elif n==29:
we.set_alpha(k)
elif n==30:
txt0f.set_alpha(k)
elif n==31:
txt0g.set_alpha(k)
#上演
mov = ani.FuncAnimation(fig,update,ends[-1],interval=50)
plt.show()